How Do You Know if a Decimal Is a Rational Number

Decimal Representation of Rational Numbers

 A rational number is a number that can be written in the form p/q where p and q are integers, and q ≠ 0. The gear up of rational numbers is denoted by Q or \(\mathbb{Q}\). Examples:one/4, −ii/5, 0.iii (or) iii/10, −0.7(or) −7/10, 0.151515... (or) 15/99. Rational numbers can be represented as decimals. The dissimilar types of rational numbers are Integers like -1, 0, 5, etc., fractions like 2/5, 1/3, etc., terminating decimals like 0.12, 0.625, 1.325, etc., and non-terminating decimals with repeating patterns (later on the decimal indicate) such as 0.666..., 1.151515..., etc.

1.	Decimal Representation of Rational Numbers
two.	Decimal Representation of Terminating Rational Number
iii.	Decimal Representation of Not-Terminating Rational Number
4.	Solved Examples on Decimal Representation of Rational Numbers
5.	Do Questions on Decimal Representation of Rational Numbers
6.	Often Asked Questions (FAQs)

Decimal Representation of Rational Numbers

The decimal representation of a rational number is converting a rational number into a decimal number that has the same mathematical value as the rational number. A rational number can be represented as a decimal number with the help of the long division method. We divide the given rational number in the long division form and the caliber which we get is the decimal representation of the rational number. A rational number tin can have two types of decimal representations (expansions):

• Terminating
• Not-terminating only repeating

Annotation: Whatever decimal representation that is non-terminating and non-recurring, will be an irrational number.

Allow's endeavor to understand what are terminating and not-terminating terms. While dividing a number by the long division method , if we become zero equally the remainder, the decimal expansion of such a number is chosen terminating.

Case: 1/2

Let us see the long division of 1 past 2 in the following paradigm:

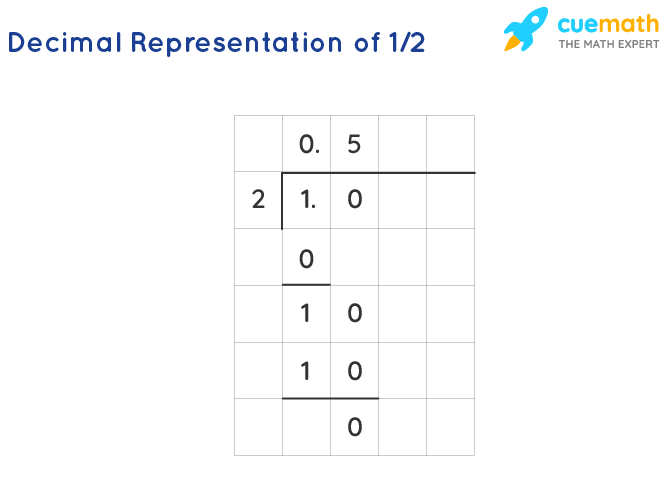
1/2 = 0.5 is a terminating decimal

And while dividing a number, if the decimal expansion continues and the rest does not become nothing, information technology is called non-terminating.

Case:  1/3

Let us encounter the long division of ane by 3 in the following image:

1/3 = 0.33333... is a recurring, not-terminating decimal. You tin can notice that the digits in the quotient keep repeating.

Decimal Representation of Terminating Rational Number

The terminating decimal expansion ways that the decimal representation or expansion terminates after a certain number of digits. A rational number is terminating if information technology can exist expressed in the form: p/(2ⁿ×5^m). The rational number whose denominator is a number that has no other gene than 2 or v, will terminate the outcome sooner or later after the decimal point. Consider the rational number 1/16.

Hither, the decimal expansion of 1/sixteen terminates after 4 digits. Here 16 in the denominator is xvi = ii⁴. Annotation that in terminating decimal expansion, you will find that the prime factorization of the denominator has no other factors other than 2 or 5.

Decimal Representation of Not-Terminating Decimal Number

The non-terminating but repeating decimal expansion means that although the decimal representation has an infinite number of digits, at that place is a repetitive pattern to it. The rational number whose denominator is having a factor other than 2 or v, will not have a terminating decimal number equally the result.

For example:

Note that in not-terminating but repeating decimal expansion, y'all will find that the prime factorization of the denominator has factors other than 2 or 5.

Related topics:

• Operations on Rational Numbers
• Rational Numbers
• Irrational Numbers

Of import Notes

1. If a number tin can be expressed in the class p/(2ⁿ×five^grand) where p ∈ Z and m,n ∈ W, so the rational number volition be a terminating decimal.
2. Terminating decimal expansion means that the decimal representation or expansion terminates after a certain number of digits.
3. Every non-terminating simply repeating decimal representation corresponds to a rational number even if the repetition starts after a certain number of digits.

1. Example 1:

   Express 1/xiii in decimal course.

   Solution:

   Permit's split 1 past thirteen.

   See the following image for the complete procedure of partition of 1 by 13.

   

   We meet that the quotient is 0.0769230769...which is a recurring decimal quotient.

   Answer: \(\begin{marshal} \frac{1}{13} = 0.\overline{076923} \cease{align}\)

2. Instance 2:

   Make up one's mind if 11/25 is a terminating or a not-terminating number.

   Solution:

   A rational number is terminating if it can be expressed in the class:

   p/(2 ^northward ×5 ^chiliad )

   The prime factorization of 25 is v×v

   eleven/25=11/(2 ⁰ ×v ² )

   Answer: xi/25 is a terminating rational number.

go to slidego to slide

Breakdown tough concepts through simple visuals.

Math will no longer exist a tough subject, peculiarly when you understand the concepts through visualizations.

Book a Free Trial Course

Ofttimes Asked Questions(FAQs)

Is a Decimal a Rational Number?

Whatever decimal number can be either a rational number or an irrational number, depending upon the number of digits and repetition of the digits. Whatever decimal number whose terms are terminating or non-terminating but repeating then it is a rational number. Whereas if the terms are non-terminating and not-repeating, then it is an irrational number.

How Do You Know if a Decimal is Rational?

Nosotros tin know a decimal number is rational or not by various methods. We can if a decimal number tin be expressed in the form p/q and q ≠ 0, then it is a rational number. Example: 0.25 = 25/100 is a rational number. Or nosotros can check the number of terms and repetition of the terms to know if information technology a rational number or not. For example, 0.33333... is a rational number.

What are the Characteristics of a Rational Number When Written as a Decimal?

When expressing a rational number in the decimal form, information technology tin be terminating or non-terminating but repeating and the digits can recur in a pattern. Example: 1/ii= 0.5 is a terminating decimal number. 1/iii = 0.33333... is a not-terminating decimal number with the digit 3, repeating.

If it is non-terminating and non-recurring, it is not a rational number.  Example:π is an irrational number since it has a value that is not-terminating and non-recurring.

Is Every Decimal Number Represented as a Rational Number?

No, every decimal number can not exist represented as a rational number. Non-terminating and not-repeating digits to the right of the decimal point cannot be expressed in the grade p/q hence they are not rational numbers. But other than these terms, all terms can be represented as a rational number or in the class of p/q.

Is 3.14 a Rational Number?

A rational number is a number that tin can exist written equally a fraction, a/b where a and b are integers, or that has terminating or non-terminating merely repeating terms. Hence, the number 3.14 is a rational number, since it has terminating terms after the decimal point. If it would have has farther terms extending to infinity, it would have been chosen an irrational number. An irrational number cannot be expressed in the form of p/q Information technology has countless non-repeating digits later on the decimal bespeak. Examples: π = 3.141592..., √2=one.414213…

What Cannot be the Decimal Representation of a Rational Number?

A decimal number, that has infinite terms where terms are not repeating itself, then information technology tin not be a decimal representation of a rational number. For a decimal number to be the decimal representation of a rational number, it should have terminating, or non-terminating just repeating terms.

How Do You lot Find the Decimal Expansion of a Rational Number?

The decimal expansion of a rational number can easily exist found out by using the long division or by only writing the rational number in the form of p/q too known every bit a fraction course. To catechumen fractions to decimals, just divide the numerator past the denominator. As it is a rational number, we will get a result that is either terminating or non-terminating simply repeating. If the denominator is of the form (2 ⁿ ×5 ^yard ), so the decimal is sure to terminate, or otherwise, it would echo with a recurring pattern.

fialasolow1942.blogspot.com

Source: https://www.cuemath.com/numbers/decimal-representation-of-rational-numbers/

Share this post